PID Control
One of the most common controllers is a PID-controller, which are currently used to control the actions of the robot. A visual representation of the system is given in Figure 1 below.
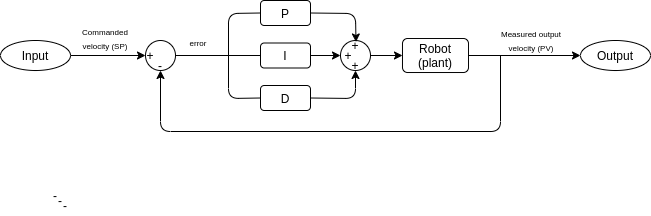
Table of Contents
Introduction
The controller tries to minimize the error by the adjustment of a control variable, which consists of a weighted sum of three control terms: a Proportional, an Intergral and a Derivative action, hence the name PID-controller. These actions can in short be explained as follows:
- Term P is proportional to the current value of the SP-PV error $e(t)$. For example, if the error is large and positive, the control output will be proportionally large and positive, taking into account the gain factor Kp. Using proportional control alone will result in an error between the set-point and the actual process value because it requires an error to generate the proportional response. If there is no error, there is no corrective response.
- Term I accounts for past values of the SP-PV error and integrates them over time to produce the I term. For example, if there is a residual SP-PV error after the application of proportional control, the integral term seeks to eliminate the residual error by adding a control effect due to the historic cumulative value of the error. When the error is eliminated, the integral term will cease to grow. This will result in the proportional effect diminishing as the error decreases, but this is compensated for by the growing integral effect.
- Term D is a best estimate of the future trend of the SP-PV error, based on its current rate of change. It is sometimes called anticipatory control, as it is effectively seeking to reduce the effect of the SP-PV error by exerting a control influence generated by the rate of error change. The more rapid the change, the greater the controlling or damping effect.
For the P action, the error $e(t)$ is multiplied by the gain $K_p$ , so $P = K_p \times e(t)$. For the I action the past errors are summed by an integral and multiplied by a gain called $K_i$ , which makes the second control action $I = K_i \times \int_{0}^{t} e(\tau) d\tau$. The third control action consists of the multiplication of controller gain $K_d$ with the rate of change in error and is described as $D = K_d \times \frac{de(t)}{dt}$. The control actions can be balanced by tuning the controller, which implies changing the gains of the three separate control actions, which regulate the so to say amount of this action.
The proportional action (P) gets the plant as fast as possible to the set-point (SP), the integral action (I) eliminates the steady state error, which is the difference between the set-point and the value that the plant (the robot in this case) converges to as a final value and the derivative control action restrains the system from moving to quickly (it dampens the systems oscillations).