Path Planning and Path Tracking

The current path planning method is called 'Bang Bang Trajectories'. Images are a bit outdated, but should still be understandable.

Trajectory is used for a continuous, smooth plan to go from A to B. Path is used for a discrete version of a trajectory, which contains some points of the trajectory. These points are used to communicate with the robot where it should go to.

This path planning tries to find a path that is time optimal. It does this with a technique called BBT (bang bang trajectories). This technique first calculates for the x and y direction separately for how long a certain acceleration is needed to arrive at the correct x or y coordinate. The calculation takes into account the current velocity, position, maximum velocity and maximum acceleration (and deceleration).

The trajectory in one dimension can consist of three types of parts: a maximum acceleration, constant maximum velocity and a maximum deceleration. This ensures that the wanted x or y position is reached as quickly as possible. So when looking at the velocity graph of a trajectory it either has a triangular or a trapezoidal shape.

This trajectory is only for one dimension though. As the robot has a maximum acceleration, the acceleration needs to be “distributed” over an acceleration in the x and y direction. By “giving” most of the acceleration to x for example, the duration of the trajectory in the x direction becomes shorter but the trajectory in the y direction becomes longer.

By plotting the distribution of the acceleration on the horizontal axis and the time that the trajectory takes on the vertical axis a graph can be made. By finding the point at which the two lines intersect, you find the trajectory that takes the shortest time to get to the target location while also taking into account the limitations of the robot.

Everything related to the creation of these BB Trajectories is currently done in the BBTrajectory1D/2D file. All these files do is create an trajectory, collision detection is not done here.

The algorithm first checks if there are obstacles on the trajectory. It does this by first converting the trajectory to a path, a series of points. After this, each line segment between two consecutive points is checked for a collision. After all different kinds of collisions are checked it will return the location, time and type of the first collision. If there is no collision, we are done.

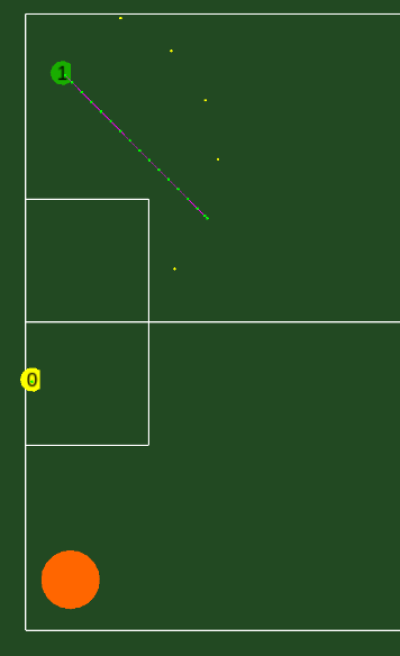
If there is a collision, some intermediate points are created on random positions on the field (for consistency, the last random point is used as well), the yellow points below. Here the robot tries to drive in a direct line towards the ball, however there is collision with the defense area. Ignore the pink/green line for now.

Now, we try to get a trajectory to the target, via an intermediate point. This happens with small steps, so first we try to move a small distance to a intermediate yellow point, see if we can make a collision free path to that point and from there a collision free path to the end location. The intermediate points are sorted based on distance to the target. As soon as a single collision free trajectory is found, we are done.

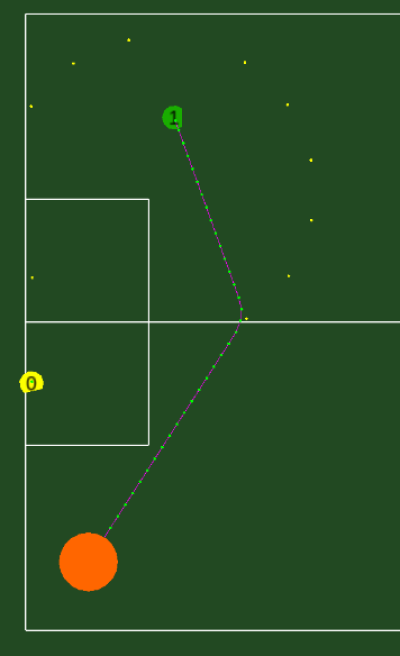
If for an intermediate point no collision free trajectory is found, we find the “best” trajectory for that intermediate point. This consist of moving for a certain time towards the intermediate point, after which we go to the target position. If for all the intermediate points no collision free trajectory is found, we pick the “best” trajectory out of all intermediate points. This is the pink/green line above. Note that this is not a trajectory to the end location, since we will change our trajectory anyways.

Now, we will follow the pink/green line. After following this path for a short while, we can find the following collision free trajectory, which we will follow to the target. Note that we don't go all the way to the yellow intermediate point, since a collision free trajectory was found before. Ever tick we redo all our paths for the planning.